Recursive Functions In Class Activity

Algebra students please click here to start the interactive recursive functions activity.

Make sure that you click "new" 2 times to generate 2 additional problems for each interactive frames and arrows problem page.

In other words, you will make rules for 3 functions on each page.

Interactive Pan Balance Game

Pan balance problems are very useful for solidifying algebraic concepts.

I found a free version of an interactive pan balance tool hosted by Utah State.  Students who are reviewing algebra concepts with me or students who cannot remember rules for solving equations should spend some time with this interactive tool.  Intuitive understanding >>>> toe memorization of rules.

The above video does a nice job of explaining how to work with this type of manipulative in order to solve an algebraic  problem.

Progression of 6th grade understanding of ratios and proportions

The 6th graders and I are winding down a very productive few weeks discussing and exploring ratios, rates and proportions.

We are taking extra time on this unit because the idea of a ratio progresses from 6th grade through freshman algebra where it becomes a linear model.  I can tell you from experience that linear models are a huge part of the algebra 1 curriculum.  A solid conceptual understanding and procedural fluency will increase the likelihood of success in future years.

And looking to college and careers later, it is important to consider that ratios and proportions are also a very common type of problem found on standardized tests like the SAT.

Here is a very brief tour of the progression of the idea of a ratio from 6th grade to high school algebra and then high school geometry.

6th grade

Ratio Tables

Double Number Lines

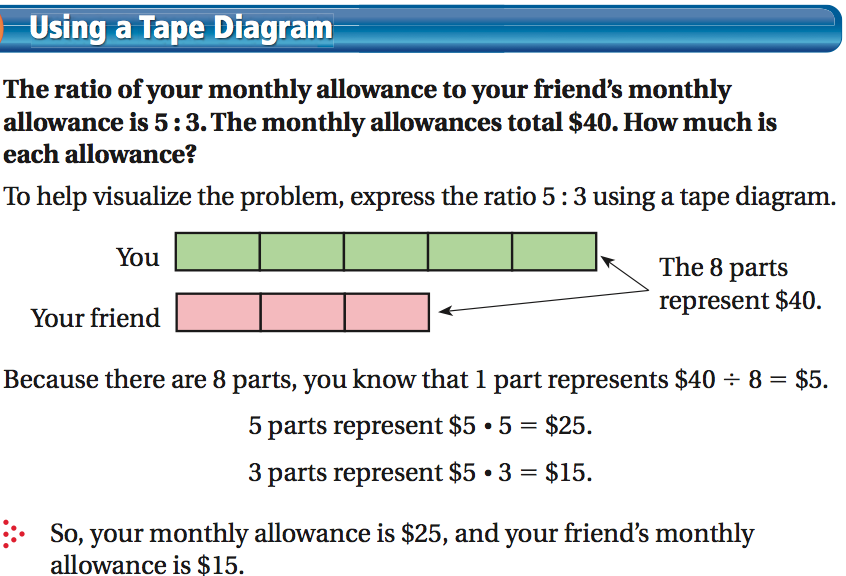
Tape Diagrams

Rates

Scale Factors/Scale Drawings

7th Grade

Ratios as Multiplicative Relationships Not Just Parallel Skip Counting

Constant of Proportionality

Graphing Proportions

8th grade and Algebra 1

Full Blown Linear Models

Extensions to High School Statistics

Extensions to High School Geometry: Similar Shapes

As you can see, ratios and proportions are a big deal and it is a good idea to make sure we get them right.

Solving a complex problem visually

I did this with a 6th grader recently.  She thought it was a very helpful intuitive explanation of how to find an average so I thought it might be fun to share.

So here go.  No crunching numbers allowed.  Let's solve this problem using only (gasp) logic and see how far we can get.

Well what is an average?  Let's think about the average numbers of beans in these cups.

Average means an even amount in each cup, so this looks like the average below.  I moved around the beans from cup to cup until there was an even number in each one.  This is the concept of an average.

Now let's make sure we can add up numbers with like units for our numbers 4 1/3, 3 1/2, 3 5/6 and 4 1/6.  Thinking of pizzas, how would you have to slice up a pizza so that 1/2 and 1/3 have the same sized slices?  

Ah, if you slice it up into six pieces then 3 slices is one half and 2 slices is 1/3.  So 1/6ths works so the numbers play nicely.  If a pizza is cut up into 6 pieces and your brother eats half and your Dad eats 1/3 then they ate 1/2 + 1/3 = 3/6 + 2/6 = 5/6 of a pizza!  You only get 1 lousy slice!

Now let's work on making even stacks to get our average.  Here are our numbers.

Let's move a few blocks around.

Not quite there though.  Let's move a few more.

Darn it!  So close.  There's not an even number of 1/6ths blocks to get exactly even stacks but we are almost there.  

This is a close up view of the very top of the stacks of blocks.  We have to divide these up evenly 4 ways.  Divide them up 4  ways ... 4 ways ... that gives me an idea ...

Um, let's divide each block up 4 ways since each one has to be shared 4 ways.  It's worth a shot.

So wait, dividing 1/6th of a pizza 4 ways means that we actually have 1/24th of a pizza.  So each itty-bitty sliver is actually 1/24th of a block.

Ok so here we see what the very top looks like when we divide those 1/24th slivers evenly.  We don't have enough to make it all the way to 4.  We are actually just one small 1/24th sliver short of 4 so we have 3 23/24 as our answer.

So there you have it folks.  The average of   4 1/3,   3 1/2,   3 5/6  and  4 1/6 

=   3 23/24 

visually.