Option to Take A Test Using IXL

Students in 4th and 6th grade have the option to prove their mastery of the most recent unit by showing their stuff on IXL rather than doing the regular test.  I spoke too soon when I offered this option to the 5th graders. The material on IXL does not match up well with what we did in class. Sorry 5th graders.

So students can begin taking the test at home tonight, continue in taking the test in class tomorrow at school and take as much time as they need in order to reach a SmartScore of 80 in each skill.

In addition to taking the test on IXL students can also use IXL as a test correction.  That is if there is an area of the test that didn't come out quite as hoped then students can demonstrated their proficiency by working on IXL.

The skills for each grade are as follows:


4th Grade Optional Assessment - IXL 4th grade tab
D2                   Factors
H1                   Functions
B2, C2            Word Problems
J4, J5               Bar Graphs
G4                   Parentheses
G6                   Algebra



6^th Grade Optional Assessment - IXL 6th grade tab
N.7                  Greatest Common Factor
N.8                   Least Common Multiple
L.1                   Divisibility Rules
L.5                   Long Division



Hope this is helpful. I like to give the students choices, especially if some students have a strong preference for keyboarding over writing by hand.

Disney Chicken Dance Video

Why is this video on my blog?  Ask your 6th grade student.

Also, because it is awesome.

Algebra 1 Functions Review

7th and 8th grade algebra students

Do this review to get yourselves ready for the test on Thursday.


Here is another useful review exercise.

This ordered pairs quiz will stretch you a little bit.

Finally one more.

6th Grade Math Jeopardy!

Best. Jeopardy. Ever.

Click here when you are at the Jeopardy station!

Zombies and Diffy Q

I feel like I have been one-upped by Woolley, et al in their paper "How Long Can We Survive?". Where my in class exercise used a linear equation to model zombie populations they used differential equations and statistics.

Show offs.  Humph.

6th grade homework log forms

This week's form is here.


The regular form is here.

Strategy Division for 6th Graders

Parents might wonder why their students would need to know strategy division which is sometimes called partial quotients division.

The answer is that I am laying bricks and building a foundation for future math content. The specific content is dividing polynomials by monomials. This is what it looks like:

It is not trivial.

So I want our current 6th graders to see that 252 divided by 6 written as

means that

    252   =    120 + 120 + 12 = 

 6             6         6       6

Now we just reduce each term!  

20 + 20 + 2 = 42

You'll notice that the above has the identical mathematical structure as dividing a polynomial by a monomial in the first example.

So it is true that your clever students can get the correct answer to 252 divided by 6 using the standard algorithm for long division.  But I want to push them farther, to reach into deeper content and link to advanced concepts. Deep understanding, advanced thinking - those are some of the reasons why you are sending your children to Kazoo School.

And strategy division is part of that formula.

Our students are awesome!

School-wide starting fluency vs. current fluency

Distribution of starting and current student fluency

Video With Detailed Step-By-Step Instructions for Long Division

I think this video is brilliant.  If you have a 6th grader please have him or her give this a glance.

Discontinuity in Oil Prices

Historical oil prices are displayed in 2012 dollars.  That is, the price each year is adjusted for inflation to be equal to the same amount of money in 2012.

Here is the original graph.

Here is the same graph with some mark ups. The mark ups make it more clear that there is not only a discontinuity in the average price level but in the volatility of prices as well.

Students interested in economic examples of discontinuous prices might want to consider looking at oil prices, especially in the 1970s. Parents, do not tell them what caused the volatility.  They can figure this out in their own.

Another Example of A Piecewise Function - Ping Response Times

The 7th and 8th Graders are doing a project on piecewise functions. Piecewise functions are ubiquitous. Any time there is a dramatic, sudden change in a process you have a piecewise function. The graphs below show two stylized, textbook examples.

Here is a real world example from the world of IT from the PingER Project at Stanford.

The graphs below show how internet response rates change due to congestion. The change in response times is not just non-linear.  There is in fact a discontinuous break in the pattern,  There are two different set of rules governing response rates when the network is not congested and when it is congested.

Students interested in computers could very easily find similar examples of research in IT that shows similar types of discontinuities.

Guided Practice for Long Division

Here are a few good sites for practicing long division:


The Great Martini Company

Math Frog

Snork's Long Division (turn down the volume on this one if practicing in class)

Divisibility Rules Quizlet Flashcards

Practice these flashcards to memorize divisibility rules.  You can play scatter, space race or do regular flashcards.

6th Grade Division Video

Go here

Recursive Functions In Class Activity

Algebra students please click here to start the interactive recursive functions activity.

Make sure that you click "new" 2 times to generate 2 additional problems for each interactive frames and arrows problem page.

In other words, you will make rules for 3 functions on each page.

Interactive Pan Balance Game

Pan balance problems are very useful for solidifying algebraic concepts.

I found a free version of an interactive pan balance tool hosted by Utah State.  Students who are reviewing algebra concepts with me or students who cannot remember rules for solving equations should spend some time with this interactive tool.  Intuitive understanding >>>> toe memorization of rules.

The above video does a nice job of explaining how to work with this type of manipulative in order to solve an algebraic  problem.

Progression of 6th grade understanding of ratios and proportions

The 6th graders and I are winding down a very productive few weeks discussing and exploring ratios, rates and proportions.

We are taking extra time on this unit because the idea of a ratio progresses from 6th grade through freshman algebra where it becomes a linear model.  I can tell you from experience that linear models are a huge part of the algebra 1 curriculum.  A solid conceptual understanding and procedural fluency will increase the likelihood of success in future years.

And looking to college and careers later, it is important to consider that ratios and proportions are also a very common type of problem found on standardized tests like the SAT.

Here is a very brief tour of the progression of the idea of a ratio from 6th grade to high school algebra and then high school geometry.

6th grade

Ratio Tables

Double Number Lines

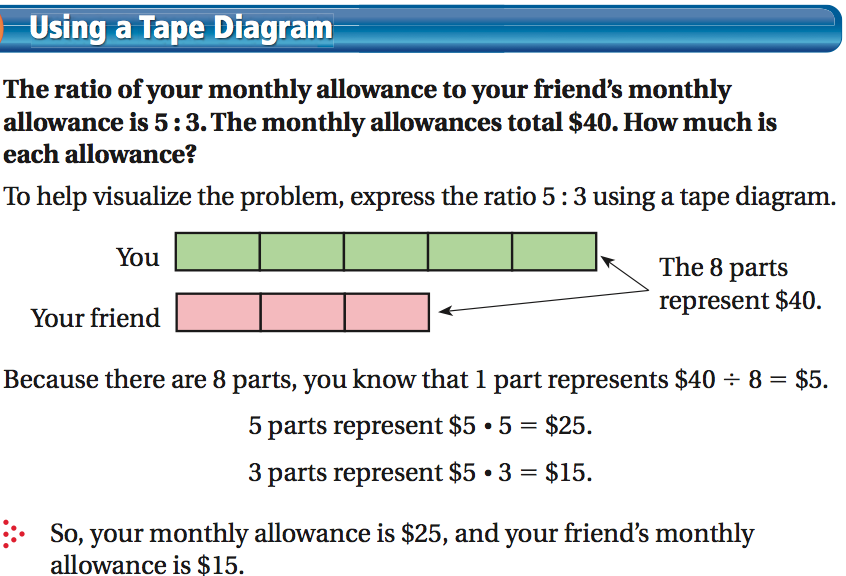
Tape Diagrams

Rates

Scale Factors/Scale Drawings

7th Grade

Ratios as Multiplicative Relationships Not Just Parallel Skip Counting

Constant of Proportionality

Graphing Proportions

8th grade and Algebra 1

Full Blown Linear Models

Extensions to High School Statistics

Extensions to High School Geometry: Similar Shapes

As you can see, ratios and proportions are a big deal and it is a good idea to make sure we get them right.

Solving a complex problem visually

I did this with a 6th grader recently.  She thought it was a very helpful intuitive explanation of how to find an average so I thought it might be fun to share.

So here go.  No crunching numbers allowed.  Let's solve this problem using only (gasp) logic and see how far we can get.

Well what is an average?  Let's think about the average numbers of beans in these cups.

Average means an even amount in each cup, so this looks like the average below.  I moved around the beans from cup to cup until there was an even number in each one.  This is the concept of an average.

Now let's make sure we can add up numbers with like units for our numbers 4 1/3, 3 1/2, 3 5/6 and 4 1/6.  Thinking of pizzas, how would you have to slice up a pizza so that 1/2 and 1/3 have the same sized slices?  

Ah, if you slice it up into six pieces then 3 slices is one half and 2 slices is 1/3.  So 1/6ths works so the numbers play nicely.  If a pizza is cut up into 6 pieces and your brother eats half and your Dad eats 1/3 then they ate 1/2 + 1/3 = 3/6 + 2/6 = 5/6 of a pizza!  You only get 1 lousy slice!

Now let's work on making even stacks to get our average.  Here are our numbers.

Let's move a few blocks around.

Not quite there though.  Let's move a few more.

Darn it!  So close.  There's not an even number of 1/6ths blocks to get exactly even stacks but we are almost there.  

This is a close up view of the very top of the stacks of blocks.  We have to divide these up evenly 4 ways.  Divide them up 4  ways ... 4 ways ... that gives me an idea ...

Um, let's divide each block up 4 ways since each one has to be shared 4 ways.  It's worth a shot.

So wait, dividing 1/6th of a pizza 4 ways means that we actually have 1/24th of a pizza.  So each itty-bitty sliver is actually 1/24th of a block.

Ok so here we see what the very top looks like when we divide those 1/24th slivers evenly.  We don't have enough to make it all the way to 4.  We are actually just one small 1/24th sliver short of 4 so we have 3 23/24 as our answer.

So there you have it folks.  The average of   4 1/3,   3 1/2,   3 5/6  and  4 1/6 

=   3 23/24 

visually.

New Homework Pages By Grade

Students request that I have separate pages for each grade's homework. And here they are!  On the right of this page are homework assignment pages for 4th -8th grade all on different pages.

The 6th, 7th and 8th grade pages have embedded videos to help them with their homework.

Fact fluency is through the roof!

Fact fluency before we started using Reflex Math (left) and after (right).

Oooooooooooh yeah ...........

8th grade in class assignment from Thursday

I extended time available for the in class assignment given on Thursday to Friday. But the assigned questions from the red algebra book are due on Friday in addition to the required work on Khan Academy.  Please turn in those questions at the beginning of Friday's class.

8th graders - in class work

There are two sure fire ways of dividing polynomials by monomials correctly.

1.  Break the polynomial in the numerator into separate up and down line-by-line problems.  Reduce each math fraction separately and then combine them at the end of the process. This method of dividing polynomials by monomials is laid out plainly here.  Do the practice problems on the next page on a separate sheet of paper.

2.  Breaking the numerator apart into separate side by side problems.  Reduce each to its simplest form and then combine.  This method is outline here.

Write down (copy) each example problem fully.



Below is another step-by-step guide on how to divide polynomials by monomials using the side by side method.

Read through the examples and then do the two practice problems.

In this case I am grading your process.  So write down each step of your solution method and label the reason for your steps exactly as done in this guide.

LearnBoost Online Grade Book

I have sent our invitations to the 4th - 6th grade parents to join LearnBoost.  By joining LearnBoost and using the provided access code you will be able to access your student's grades on quizzes, tests and homework.  I will send out 7th and 8th grade invitations soon.

Please do not worry if your student has a poor grade on a quiz or test.  I have an unlimited retake policy and encourage students to keep coming back to a topic until they master it.

New videos uploaded to the 7th grade videos page

Combining like terms

This week - 8th grade

Monday:  factoring trinomials with a leading coefficient of 1 lecture, notes, guided examples and practice

Wednesday: factoring trinomials review and activity

Thursday:
Practice and review of factoring
Quiz 3, Factoring GCF, Perfect Squares, Trinomials
Quiz Retakes during class when Quiz 3 is finished

Friday:

Return Quiz 3
Lecture, notes and guided practice on factoring trinomials with a non-zero leading coefficient,

This week 7th Grade

Monday: Quiz 2 on Order of Operations and Expressions

Wednesday: Combining Like Terms Lecture, Notes and Guided Examples

Thursday: Combining Like Terms Whole Class Review and Activity

Friday: Simplifying Expressions

Quiz on Wednesday October 22, 2014

What we are doing this week - 6th grade Ratios and Proportions

8th graders - dividing a polynomial by a monomial

All of you need to practice this skill.

Here is a Khan Academy video explaining the steps to simplifying this type of expression.

My advice is that when you see this type of problem written like (4x^2 - 5x + 10) ➗2x convert it into fractional form with a numerator and denominator:

4x^2 - 5x + 10

----------------

         2x

What I am reading - Perceptual Learning

I am very interested in the psychology of learning. I was Googling around today to try to nail down the difference between associative learning and pattern recognition (there is a difference) and came upon this little gem (Kellman et al, 2010).

I have observed students learning through exposure to correct solutions without an explicit explanation but have not had a framework for understanding this process. From page 7:

Implicit pattern recognition versus explicit knowledge. Although PL may provide important scaffolding for explicit, verbalizable knowledge, PL itself need not involve explicit knowledge. PL changes the way a learner views a problem or representation; this idea of ‘‘mind as pattern recognizer’’ (Bereiter & Scardamalia, 1998) need not be accompanied by explicit facts, concepts, or procedures. In some domains, one might be able to demonstrate a ‘‘double dissociation’’ between PL effects and effects of con- ventional instruction. Whereas conventional instruction may lead to verbalizable knowledge but lagging pattern recognition and fluency, PL may produce the reverse. Such a clear division, although imaginable, may in practice be difficult to observe, because these forms of learning are normally synergistic, producing performance out- comes in which pattern recognition, facts, concepts, and procedures interact.  

There is much more to this. One very interesting insight is that students using PL methods will be able to "see" the solution prior to being able to verbalized the rationale for the solution method.

Learning is a very weird process and that makes teaching hard.


Kellman, Philip J., Christine M. Massey, and Ji Y. Son. "Perceptual learning modules in mathematics: Enhancing students’ pattern recognition, structure extraction, and fluency." Topics in Cognitive Science 2.2 (2010): 285-305.